Mechanical desktop calculating machines, mid-20th Century

A mechanical calculator or calculating machine was a mechanical device for performing basic arithmetic, generally by the turn of a handle or pull of a lever. These machines eased the task of lengthy calculations before electronic calculators and computers were commonplace. This page describes and the workings of a typical such calculator, the Brunsviga 13RK, and explains how it was used for quite complex calculations.
____
By Neil Cryer who regularly used a mechanical calculator while working in a laboratory in the 1950s.
Main parts of the Brunsviga 13RK
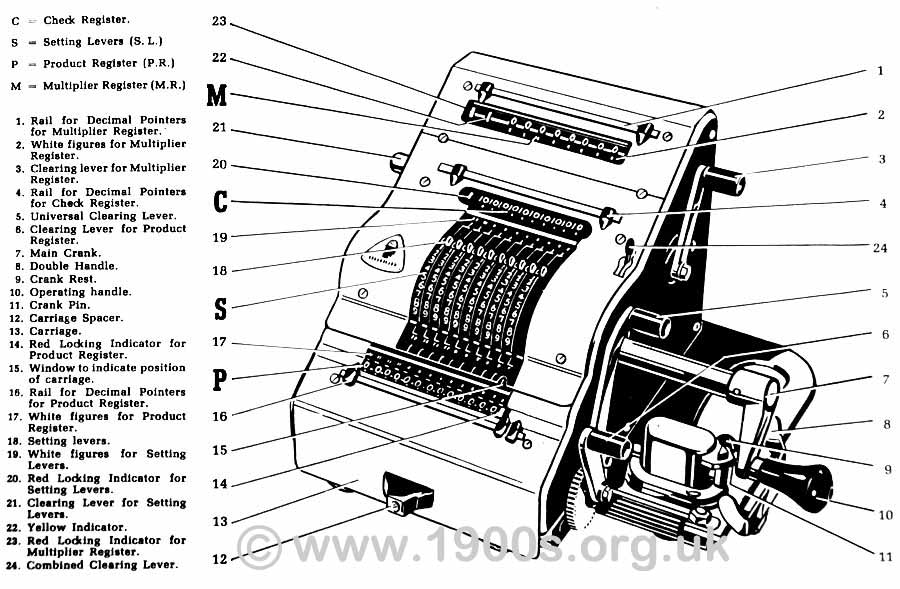
Labelled parts of the Brunsviga 13RK.
Types of mechanical calculating machine
There were several makes of these mechanical calculators, and a mechanical calculator of sorts could be found in most large offices and laboratories.
The one that I used was a Brunsviga 13RK - see the photograph - which was particularly sophisticated. It is still in my possession because I rescued it when it was about to be thrown out.
How mechanical calculating machines worked
What follows in this section is very much a simplification of how mechanical calculators worked, but it will serve as a basis for explaining what the calculators were like to use, which is in the next section.
Addition and subtraction by mechanical calculator
At the heart of a typical mechanical calculator was a rotatable drum turned by the large handle at the side. This drum consists of a set of identical discs with 0 to 9 printed round their circumference. If the drum held, say, 6 discs, then it could be set to hold any six digit number. For instance the number 125 would be set by adjusting successive discs to show 000125. If you were to see inside the calculator you would see that the disc marked 1 would currently have 1 lump sticking out. The disc set to 2 would currently have 2 lumps sticking out etc.
Alongside the main drum were two mechanical displays which were initially set to zero. One displays the number of times the main drum has turned, the second displays the result of the calculation.
The second 'results' display is special in that if you now turn the main drum once you will find this results display has made a clicking noise and now holds the exact same number as on the main drum, i.e. you have 'added' the drum number to the results display. If you were now to turn the handle backwards you would hear the same sort of clicking noise as before but see that the results display has now gone back to zero. You have subtracted 125 from 125 to give 0.
Page from the manufacturer's instruction booklet showing how to add. Subtraction begins on this page.
Continuation showing how to subtract.
Multiplication by mechanical calculator
As described above one turn of the drum added the drum number to the results display. A second turn of the handle would add the same number again. Multiple turns of the handle would add the number set on the drum multiple times to the results display. The results display would then hold the number set on the drum multiplied by the number of times the drum was turned which is also show on its own turns display.
ie [turns display] x [drum number] = [results display]
ie [2] x [125] = [250]
The real power of the mechanical calculator is that the relative position of the main drum can be shifted sideways a distance of one digit at a time. This is the equivalent of multiplying the drum number by 10 at a time. If the number set on the drum was 125 and it was then shifted left one digit it would now represent 1250. At the same time the display showing the number of rotations has also shifted left resulting in each rotation of the drum to register as 10 rather than the 1 it would have registered had there been no shift left.
Multiplication of a multi digit number by a second multi digit number is a simple matter of setting up one number on the drum and then turning the handle and shifting left to produce the second number on the turns display. The varius displays will then reveal:
ie [turns display] x [drum number] = [results display]
Division was achieved by a form of subtraction with the handle turned in the reverse direction. I will not try to describe it here but to help anyone pondering on the matter I will point out that if the results display goes negative then a bell rings. At that point the drum should be rotated one turn forwards.
Trust me, it is very simple when you are used to it, but is easier to demonstrate than to put into words. If you would like a thorough explanation for the Brunsviga 13RK, the first few pages of the manufacturer's instruction booklet are in large legible images. Just tap/click the thumbnails.
More capabilities of the Brunsviga 13RK
The was capable of more than simple addition, subtraction, multiplication and division: it could also do square roots, percentages and currency conversions. The following are just two examples.
Page showing how to handle fractions and decimals
More about using the Brunsviga 13RK
Pros and cons of mechanical calculating machines
When you realise that back in the 1950s few people could imagine electronic calculators, the advantages of mechanical calculating machines were considerable. Slide rules were quick to use but only really accurate to two or at best three significant figures, and the most common books of tables were accurate to four significant figures. In contract, mechanical calculators were accurate to as many figures as there were rotors. In the case of the Brunsviga 13RK, this meant that a calculation could be accurate to nine significant figures.
On the negative side, though, calculations were time consuming. Remember that to multiply by nine, for example, the handle had to be turned nine times. Also as the machines contained a lot of metal and were precision-made, they were too expensive to buy in bulk. So one was not always to hand when needed because someone else was using it. Furthermore the machines were very heavy to move and were not exactly quiet in operation.
To be fair, users quickly got used to the negative aspects of these mechanical calculating machines. What we didn't know, we didn't miss. Also, for someone of the same turn of mind as me, there was a fascination about them and an admiration for how they worked.
Shortcuts
contributed by Greg Everard, personal experience
Under the disadvantages mentioned above is the large number of turns needed to multiply by 9. We used the Brunsviga calculators in technical college for a numerical analysis course in the late 1960s in the UK and were taught some shortcuts, most of which I forget now. I do remember, though, that any number over 6 was handled by left shifting to next wheel and turn once (multiply by 10) then right shift back and REVERSE wind the complement of the number e.g. once for 9, twice for 8 etc. So, to multiply by say 98, we left shifted twice and rotated once to multiply by 100 then right shifted back to the units and reverse wound twice. We could of course do the reverse wind first, then we only needed to do the shift operation once but this meant a large number of pins being moved as the full register was tripped backwards before again moving them all forwards, so it didn't really save any effort and was harder on the machine.
Alternatives to calculating machines
There were alternatives at the time: slide rules, and books of tables, but of course none were electronic.
| sources | webmaster | contact |
Text and images are copyright
If you can add anything to this page or provide a photo, please contact me.







